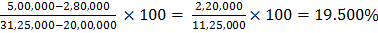Everything you need to know about the techniques and methods of capital budgeting.
Capital Budgeting or Investment Decisions or Capital Expenditure Decisions may be defined as a firm’s decision to invest its current funds most efficiently in the long term assets in anticipation of an expected flow of series of years.
Such decisions are very important for a firm, since a considerable amount of funds has to be committed to the long term assets.
ADVERTISEMENTS:
Capital budgeting is a process of planning capital expenditure which is to be made to maximize the long-term profitability of the organization.
Capital budgeting is a long-term planning exercise in selection of the projects which generates returns over a number of years in future and the heavy expenditure is to be incurred in the initial years of the project to generate returns over the life of the project.
The techniques and methods of capital budgeting can be classified into traditional and discounted cash flow techniques.
Some of the techniques and methods of capital budgeting are:-
ADVERTISEMENTS:
1. Payback Method 2. Average Rate of Return Method 3. Net Present Value Method 4. Internal Rate of Return Method 5. Profitability Index Method 6. Urgency Method 7. Unadjusted Return on Investment Method 8. Present Value Method 9. Terminal Value Method 10. Benefit-Cost Ratio Method.
Additionally, learn about the examples, formula, advantages, disadvantages, accept-reject criterion and suitability of the capital budgeting techniques.
Capital Budgeting Techniques: Importance, Process and Modern Methods (with Advantages and Disadvantages)
Techniques of Capital Budgeting – With Formula, Examples, Advantages and Disadvantages
The methods and techniques of capital budgeting can be classified into two types:
ADVERTISEMENTS:
1. Traditional, and
2. Discounted cash flow techniques,
The first category includes:
ADVERTISEMENTS:
(a) Payback Method, and
(b) Average Rate of Return Method
The second category takes the time factor into account, and it includes:
(a) Net Present Value Method,
ADVERTISEMENTS:
(b) Internal Rate of Return Method, and
(c) Profitability Index Method.
1. Traditional Method:
(a) Pay Back Method:
This is the traditional method, simplest and the most widely used method for appraising capital expenditure decisions. The term pay back or pay out or pay off, refers to the period in which the project will generate the required CFAT (that is, cash flows, after taxes) to recoup the initial investment. There are two methods of calculating the payback period.
ADVERTISEMENTS:
(i) When Cash Flows are Uniform:
If the cash flows are uniform for each year of the project’s life, that is, if CFAT’s are uniform, then the payback period is calculated using the equation –
Payback period = Investment / Constant annual cash inflow
For example- if a project requires an investment of Rs. 20,000 and is expected to produce CFAT of Rs. 5,000 for 10 years, then the payback period –
ADVERTISEMENTS:
= 20,000 / 5,000 = 4 years.
This signifies, that the investment in the purchase of the machine, will be recovered in 5 years.
In this situation, payback period is calculated by the process of cumulative cash flows, till the time when cumulative cash flows become equal to the original investment.
This method where cash flow for each year may be different can be explained with the help of the following examples:
Problem 1:
ADVERTISEMENTS:
A project requires an initial investment of Rs. 20,000 and annual cash inflows (CFAT) for 5 years are Rs. 6,000, Rs. 8,000, Rs. 5,000, Rs. 4,000 and Rs. 4,000 respectively.
The calculation is explained with the following table:
The above table shows that in three years, Rs. 19,000 has been recovered and Rs. 1,000 is left out of initial investment. In the fourth year the cash inflow is Rs. 4,000. It means that the payback period is between three to four years. To calculate the fraction, we have to divide the amount of funds needed to recover the investment in the fourth year, by the amount of cash flow in that year, that is, 1,000 / 4,000 in our example. So the interpolated payback period is 3 years + (1,000 / 4,000) = 3.25 years.
Accept-Reject Criterion as per the Pay Back Period:
The payback period can be used as a criterion to accept or reject an investment proposal.
The following are the rules for decision making as per this method:
(i) A project whose annual pay back period is more than what has been pre-determined by the management will be straight away rejected. The fixation of payback period is generally done by taking into account the, reciprocal of the cost of capital. For example- if the cost of capital is 20%, the maximum acceptable payback period would be fixed at 5 years
(ii) In the case of mutually exclusive projects, pay back can be used as a ranking method. Here, the projects are ranked according to the length of the payback period. Thus the project having the shortest pay back may be assigned rank one, followed in that order, so that the project with the longest pay back, would be ranked the lowest. Then the projects with the shorter payback period will be selected.
Advantages of Pay Back Period Method:
(i) This method is very useful in evaluating projects which involve high uncertainty. Due to the risks and uncertainty involved, payback period rejects projects with a payback period over five years.
(ii) Secondly, the firm will start getting profits once the payback period is over. So the firms can plan their profit appropriation in advance.
(iii) This method reduces the possibility of loss on account of obsolescence because as per this method, earlier benefits are better than later benefits and investment decisions are made accordingly.
Disadvantages of Pay Back Period Method:
This method has the following demerits:
(i) The first drawback of this method is that it completely ignores all cash inflows after the payback period. As per this method, projects having long gestation period are always rejected, even if the project may give high returns for a long period, this can be made clear with the following example –
As per the pay back method, both the projects would be given equal ranking, which is apparently incorrect. Here the cash flow for Project A stops at the end of the third year, while that of B continues upto the fifth year. Obviously project B is better for the firm, because it continues to give Rs. 3,000 each, for the 4th and 5th year. So the Payback period cannot be regarded as a measured of profitability, that is, this method does not consider the total benefits accruing from the project.
(ii) This method does not take into account time value of money. In other words, this method ignores the fact that a rupee tomorrow, is worth less than a rupee today.
This can be made clear with the help of the following example:
The payback period is three years in both the cases. However project A should be preferred as compared to project B, because of speedy recovery of the initial investment.
(iii) Scrap value and life of the project are not considered in calculating the payback period.
Suitability of the Pay Back Period Method:
The payback period method is suitable in the following cases:
(i) This method is appropriate for firms suffering from a liquidity crisis. In such a situation, the pay back method can be used as selection criterion, because as per this method, earlier benefits are better than later benefits.
(ii) The payback period method is helpful in taking capital budgeting decisions for the firms which give more emphasis for short term performance, rather than long term growth.
(iii) Where the project carries high risks and only the immediate future can be predicted.
(iv) When the project is financed with money borrowed at very high interest and quick returns are essential for speedy repayment of borrowed funds.
(v) In the case of an industry with high rate of technological obsolescence.
(vi) In the case of investments abroad, where the political stability, can be foreseen only for a limited number of years. For example- for investments in Pakistan, Iraq or Afghanistan.
(b) Average Rate of Return Method (ARR Method):
The accounting rate of return (ARR) method is also known as the Return on Investment (ROI) method. This method uses accounting information as revealed by the financial statements, to measure the profitability of an investment.
The Average Rate of Return (ARR) is calculated using the following equation:
This averaging process assumes that the firm is using straight line method of depreciation therefore the book value of the asset declines at a constant rate from its purchase price to zero at the end of its depreciable life.
This is because the amount required for additional net working capital (that is, current assets – current liabilities) remains tied up, during the life time of the asset. Its entire amount is thus a part of investment in the asset.
This method is an improvement over the payback period method, because this method considers the earnings from a project over its entire economic life.
Accept Reject Rule as per ARR Method:
The calculated ARR is compared with the cut off rate. Cut off rate is decided by the management well in advance, i.e., it is the rate of return on investment that should be generated from a project and this is usually the firm’s cost of capital.
If the return on investment of a project, is less than the cut off rate of return, the investment proposal is rejected straight away. On the other hand, if the return on investment of a project is equal to or more than the cut off rate, the project becomes acceptable. The acceptance rule is –
Accept if ARR > Minimum Rate and Reject if ARR < Minimum Rate
In the case of mutually exclusive projects, the project with the higher ARR would be preferred, over projects which have lower ARR.
Advantages of ARR Method:
(i) This method is simple to calculate if accounting profits after taxes are easily obtainable, moreover, it is simple to understand and use.
(ii) The total benefits form the project are taken into account for calculating ARR, whereas, in the case of Pay Back Period, benefits after the payback period are not considered.
(i) As per this method, calculation is based on the accounting profit instead of cash flows. It has been already explained, of the superiority of cash flows over accounting profit in capital budgeting decisions.
(ii) Secondly, this method ignores the time value of money. Accordingly benefits in the earlier years and later years are valued equally. This is another drawback of ARR method.
(iii) Thirdly, the ARR method of measuring the worth of the investment does not differentiate between the sizes of the investment required, for each project.
Different proposals may have the same ARR, but may require different average investments as shown below:
Here ARR is 20% for all the projects, but each project needs different investments. In such a situation a firm may find it difficult to take a rational decision.
2. Discounted Cash Flow Methods:
These methods are also known as time adjusted techniques. These methods take into consideration, the time value of money while evaluating the costs and benefits of a project, that is, the cash flows associated with the project, are discounted at the cost of capital. Another important feature of discounted cash flow method, is that it takes into account all benefits and costs, occurring during the entire life of the project.
Let us explain the methods in detail:
(a) NPV Method or Net Present Value Method:
The calculation can be divided into two stages. The first stage involves the determination of an appropriate rate of discount. Generally cost of capital is used as the discounting rate. Then the cash inflows and outflows associated with each project are worked out, and the difference between the two is the Net Present Value or NPV.
Thus NPV may be defined as, “the summation of the present values of the cost proceeds (CFAT) in each year, minus the summation of present values of the net cash outflows in each year”.
Advantages of NPV Method:
(i) This method considers all cash flows.
(ii) This method recognises the time value of money.
(iii) This method is consistent with the wealth maximisation principle.
(iv) This method is more scientific and dependable.
(v) This method makes it possible to compare projects requiring different capital outlays, having different number of years of life, different timings of cash flows, all at a particular moment of time, by discounting all the cash flows.
(vi) This method is particularly useful for the selection of mutually exclusive projects.
Disadvantages of NPV Method:
(i) This method is difficult to calculate and understand with the calculations involved.
(ii) This method requires estimates of cash flows, which is a tedious task.
(iii) Another drawback of this method is the calculation of the required rate of return, to discount the cash flows. Moreover, different discount rates will give different present values and the relative desirability of a proposal will change with a change in the discount rate.
(iv) While deciding in the case of two projects, this method will favour the project which has the higher NPV. But it also possible, that this project may require larger initial outlay. Thus, in the case of projects involving different outlays, the present value method may not give dependable results.
Accept-Reject Rule as per NPV Method:
The decision rule for a project under NPV method, is to accept the project if the NPV is positive, and reject if it is negative. Symbolically –
NPV > Zero- accept
NPV < Zero- reject.
In the case of mutually exclusive projects, project with the highest positive NPV is accepted.
(b) Internal Rate of Return Method:
This is a discounted cash flow or time adjusted method, for evaluating the capital investment decisions. This method also considers the time value of money, by discounting the cash flows. But in the case of the present value method, the discount rate is the cost of capital that is pre-determined. Determining the cost of capital for present value method is external to the proposal under consideration.
On the other hand, for IRR, it depends entirely on the initial outlay and the cash proceeds of the project which is being evaluated, for acceptance or rejection. That is, the IRR is based on facts, which are internal to the proposal that is the reason why it is called the Internal Rate of Return. This method is also known as Yield on Investment, Marginal Efficiency of Capital, Marginal Productivity of Capital, Rate of Return, Time Adjusted Rate of Return etc.
Internal rate of return is the rate at which the total of discounted cash inflows equals the total discounted cash outflows-that is, the rate of discount which reduces the net present value of an investment to zero, it is defined as “the discount rate which equates the aggregate present value of the net cash inflows (CFAT), with the aggregate present value of cash outflows of a project.” In other words, internal rate of return is usually the rate of return that a project earns.
Using Internal Rate of Return, selection of a project is made as follows:
(i) In the case of an independent or single investment or project, if the internal rate of return is higher than the cut off rate or hurdle rate, the project will be approved or vice versa.
(ii) In the case of mutually exclusive projects, the project, which has the highest internal rate of return, is selected, provided its internal rate of return is more than the cut off rate and the other projects will be rejected.
(iii) If there are budget constraints, the projects will be ranked in the descending order of internal rate of return and the project with the highest internal rate of return will be selected, subject to the availability of funds.
Internal rate of return is calculated using two methods, on the basis of nature of cash flows and with the present value tables that is –
(i) When cash inflows are uniform, and
(ii) When cash inflows are not uniform.
(i) When Cash Inflows are Uniform:
If cash inflows are uniform, first the factor has to be located using the equation –
(ii) When Cash Inflows are Not Uniform:
Here also IRR involves a trial and error procedure. In this process, cash inflows are to be discounted by a number of trial rates. The first trial rate may be calculated on the basis of the same formula, which is used for determining the internal rate of return when cash inflows are uniform. The only difference is that here ‘C’ stands for annual average cash inflow, instead of annual cash inflow. Symbolically –
F = 1 / C = Initial investment / Annual average cash inflow
After applying the first trial rate, the second trial rate is determined when the total present value of the cash inflows is greater, or less than the total present value of cash outflows. If the total present value of cash inflows is less than the total present value of cash outflows, the second trial rate taken will be lower than the first rate.
But if the present total value of cash inflows exceeds the present total value of cash outflows, a trial rate higher than the first trial rate will be used. This process will continue till the cash inflows and outflows, more or less set off each other. This rate will be the “Internal Rate of Return”.
Advantages of IRR Method:
(i) This method is easy to calculate and makes it simple to evaluate the investment proposals.
(ii) This method considers the time value of money.
(iii) This method considers all cash flows.
(iv) This method is not in conflict with the concept of maximising the wealth of the equity shareholders.
Disadvantages of IRR Method:
(i) This method requires the estimates of all cash inflows, which is a tedious work.
(ii) The result of IRR Method may be sometimes in conflict, with the result of NPV method. This is especially true in case of mutually exclusive projects, where IRR method may suggest to accept one project and the NPV method may suggest to reject the project.
This conflict may be due to the following factors:
(a) Different initial investments,
(b) Unequal lives of projects,
(c) Different pattern of cash flows (that is, conventional and non-conventional).
(iii) Another drawback of this method is that if tried with different trial rates, the final answer will be different.
Comparison of the Internal of Return Method with Net Present Value Method:
Both the methods are based on discounted cash flow techniques, but the differences between these two methods are the following:
1. The Net Present Value Method takes the interest rate as a known factor, while Internal Rate of Return Method takes it as an unknown factor.
2. The NPV method seeks to find out the amount that can be invested in a given project, so that, it’s anticipated earnings will be sufficient to repay this amount with interest, at that market rate. But the IRR method seeks to find out the maximum rate of interest, at which the funds invested in the project would be repaid, out of the cash inflows arising out of that project.
3. Both the methods are based on the assumption that, cash inflows can be reinvested at the discounting rate in the new projects. But reinvestment of funds at the cost of capital is more possible, than at internal rate of return. Therefore, NPV method is more reliable than the IRR method for ranking two or more capital investment projects.
Similarities in Results under NPV and IRR:
Both the methods will give the same results for investment proposals in the following cases:
1. Projects with Conventional Cash Inflows:
That is, when an outflow is followed by a series of cash inflows.
2. Independent Investment Proposals:
That is, for single investment proposals. The reason for similarity in results is simple, because in the case of NPV method the proposal is acceptable if NPV is positive. NPV will be positive, only when the actual rate of return on investment is more than the cut off rate. Similarly in the case of IRR method, a proposal is acceptable, when the IRR is higher than the cut off rate.
Thus both methods will give consistent results, since the acceptance or rejection of the proposals under both the methods, are based on the actual return being higher than the cut off rate.
Conflict in Results under NPV and IRR:
Both the methods may give conflicting results in the case of mutually exclusive projects, that is, where acceptance of one project would result in non-acceptance of the other.
Such conflict of result may due to any one or more of the following reasons:
1. When the project require different cash outlays.
2. When the projects have unequal lives, and
3. When the projects have different patterns of cash flows.
In such a situation, the results as per the NPV method should be accepted, because this method considers the total yield on investment that means the objective of this method is to maximise the wealth of the shareholders.
But IRR method is concerned with the rate of return on investment, rather than the total yield on investment. Therefore, in the case of mutually exclusive projects, the project with the highest NPV will have a beneficial effect on shareholder’s wealth.
Advantages of Discounted Cash Flow Methods:
1. Discounted cash flow methods take into account the time value of money; therefore, these methods are theoretically better than non-discounted cash flow methods.
2. Discounted cash flow methods takes into account directly, the amount of expenses and revenues over the project’s entire life. In non-discounted cash flow methods, averages are taken.
3. This method gives more weight to those money values which are nearer to the present period than those which are away from it. But in the case of other methods money units are given the same weights which are unrealistic.
4. This method makes possible the comparison of projects, requiring different capital investments, different lives, different timings of cash flows, etc., at a particular moment of time, by discounting all cash flows.
Disadvantages of Discounted Cash Flow Methods:
1. This method is difficult to understand and work out, as compared to other methods, of ranking capital investment proposals.
2. The method takes into account only the cash inflows, on account of a capital investment decision. But profitability of a capital proposal is equally important, which can be judged only when the net income, (and not the cash inflows) on account of the operation is considered.
3. This method is based on the assumption that, cash inflows can be invested at the discounting rate in the new projects. But this assumption is not always good, because it all depends upon the available investment opportunities.
Profitability Index (PI) is the ratio of investment to payoff of a suggested project. It is a useful capital budgeting technique for grading projects, because it measures the value created by per unit of investment made by the investor.
This technique is also known as Profit Investment Ratio (PIR), Benefit-Cost Ratio and Value Investment Ratio (VIR).
The ratio is calculated as follows:
Profitability Index = Present Value of Future Cash Flows/Initial Investment
If project has positive NPV, then the PV of future cash flows must be higher than the initial investment. Thus the Profitability Index for a project with positive NPV is greater than one and less than one for a project with negative NPV.
This technique may be useful when available capital is limited and we can allocate funds to projects with the highest Profitability index.
If Profit Index is greater than one, then project should be accepted.
If Profit Index is less than one, then reject the project.
Techniques of Capital Budgeting – Traditional and Modern Methods (With Procedure of Calculation)
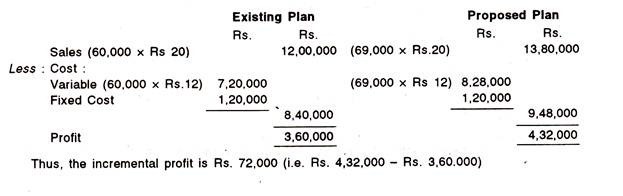
The management of an organization closely evaluated the specific financial implications of an investment decision and applies several different evaluation methodologies to the supply expected financial data that is produced through a thorough researching of the different costs and benefits associated with the acquisition.
The proper use of evaluation techniques and criteria should enable management to make more effective decisions which result in future success.
There are several of methods for evaluating capital expenditure projects which are listed below:
Technique # 1. Traditional Method:
I. Pay Back Period:
Pay-back period refers to duration required to recover amount spent in an investment proposal. Payback period is a traditional and the most simple method of capital budgeting. The basic essence of this method is to determine the amount of time that is required to recover the funds spent on the investment proposal.
Procedure for Calculating Pay-Back Period:
Pay-back period calculation is based on cash flows generated from the investment proposal and amount spent on investment proposal. Therefore we need initial investment and cash flows to calculate pay-back period. However it is important to note that series of cash flows generated from investment proposal can be same (even) throughout the life of the investment proposal or it may vary year on year (uneven).
Therefore based on the series of cash flow the procedure to calculate pay-back period also slightly varies:
Situation 1- Even Cash Flows:
When the cash flows generated from the investment proposal are same thought its life, the following equation is used to determine pay-back period.
Annual Cash flows = Cash flow before Depreciation after Tax (CFBDAT)
Situation 2- Un-Even Cash Flows:
When the cash flows generated from the investment proposal varies throughout its life, the following steps should be followed.
i. Write down the years and cash flows from the investment proposal parallel.
ii. Calculate cumulative cash flows- this can be done by continuous adding the cash flows generated from the invest proposal year after year till we reach initial investment.
iii. In case if the cumulative cash flows exceeds initial investment, then following formula can be used to determine exact pay-back period-
Acceptance and Rejection Criteria:
In case of independent investment proposals we have to compare the pay-back period of the proposal with the expectation of management (also called standard or cut-off rate). If the PBP is less than or equal to cut off rate proposal should be selected, if not rejected. In case of mutually exclusive proposals, we have to compare payback period of all the proposals and whichever proposal has a lesser PBP should be accepted.
However if cut off rate is given and if it’s a mutually exclusive proposal then all the proposals should be evaluated keeping in mind the expectation of the management.
II. Post Pay-Back Method:
Post pay back method is an improvement of payback period method. One of the major drawback of pay-back period method is that it does not consider the cash flows earned after pay-back period and as a result of this the true profitability of the investment proposal cannot be judged. Therefore in post pay back method the cash flows or returns earned after recovering initial investment is taken as a criteria for accepting and r ejecting investment proposal.
Procedure for Calculating Pay-Back Period:
In post payback method sum total of cash flows recovered from investment proposal during its economic life in taken into consider.
The following equation can be used to determine post payback profit:
Post pay back profit = Total of sum total of cash inflows – Initial investment
Cash flows means Cash flow before Depreciation after Tax (CFBDAT)
Acceptance and Rejection Criteria:
In case of independent proposal, if the proposal generates profits after recovering initial investment during its economic life it should be selected, if not rejected. In case of mutually exclusive proposals after making comparison whichever proposal yields high profits post recover of initial invest should be selected.
Evaluation of Post Pay-Back Period Method:
Post Payback profit method is simple and easy to understand and compute. Further it gives more importance on profitability for making decision about the investment proposals. Despite of its merits this method just like payback period ignores the time value of money. Further the post payback method focuses on short-term profitability, an attractive proposal could be overlooked if the profitability is the only consideration.
III. Accounting Rate of Return:
In this method the profits earned on the amount of investment proposal is expressed in terms of percentage, hence this method is also called Return on investment method. Thus accounting rate of return divides the average profit by the average investment in order to get the ratio or return that can be expected. This allows enterprise to easily compare the profit potential of investment proposals.
Procedure for calculating accounting rate of return:
i. The first step is find out the average annual cash flows, average annual cash flows here indicates cash flows earned from the investment proposal during its economic life divided by period of cash flow generation. The cash flows are averaged to ensure that balance between variations in cash flows received from the project during its economic life. Therefore average annual cash flow = Sum of cash inflows during the economic life of the investment proposal after depreciation and tax – period of cash flow generation.
Cash flows means – Cashflow after Depreciation after Tax (CR4DAT), one of the reason for terming this method as accounting rate of return is because this method is based on conventional accounting concept as it takes accounting profits as cash flows (depreciation is not added back.)
ii. The second step is to determine average investment, this is calculated by using any of the following equation.
Which is the Most Appropriate Equation?
The third equation is more appropriate to calculate because estimated value that an asset will realize upon its sale at the end of its life is considered further assets require additional working capital to operate (taken into account at the beginning of the project when calculating the initial investment).
On account of termination of project or end of asset’s life, working capital requirement associated with asset or project also ends resulting in the cash inflow. This means the working capital utilized during the life of the project or asset will be realizable by the firm. In case working capital is not given it is advisable to use equation 2, in case working capital is given it is advisable to use equation 3.
Acceptance and Rejection Criteria:
In case of independent investment proposals we have to compare ARR of the proposal with the expectation of management (also called standard or cut-off rate). If the ARR is more than or equal to cut off rate proposal should be selected, if not rejected. In case of mutually exclusive proposals, we have to compare ARR of all the proposals and whichever proposal has a higher ARR should be accepted. However if cut off rate is given and if it’s a mutually exclusive proposal then all the proposals should be evaluated keeping in mind the expectation of the management.
Evaluation of Average Rate of Return Method:
The Accounting Rate of Return method is one of the most widely used techniques for investment appraisals and capital budgeting decisions. The accounting rate of return calculation is based on the return of the investment proposal and divides the average profit by the average investment in order to get the ratio or return that can be expected. In terms of reaching a decision, a simple method is to accept any project that has an accounting rate of return that is higher than the cost of capital.
Merits of Accounting Rate of Return Method:
1. Simple and straightforward to compute.
2. Based on accounting information and thus special reports are not required.
3. Recognizes the profitability factor of investment.
4. Offers a certain degree of comparability between projects.
5. Takes all the years into account when making an investment decision.
Demerits of Accounting Rate of Return Method:
1. No account of time value of money.
2. It can be calculated in different ways. Thus there is problem of consistency.
3. It ignores the reinvestment potential of a project.
4. The accounting rate of return does not remain constant over useful life for many projects. A project may, therefore, look desirable in one period but undesirable in another period.
5. It uses accounting figures which can be affected by judgment, accounting policies and non-cash items (depreciation).
Technique # 2. Modern Method:
I. Net Present Value Method:
This method is used by most of the large companies to evaluate investment projects. One of the important feature of Net Present Value method is that it takes into account Time value of money. The concept of time value of money advocates that money available at the present time is worth more than the same amount in the future due to its potential earning capacity.
The concept behind the NPV method is simple. When firms make investments, they are spending money that they obtained, in one form or another. The money can be obtained from investors or from a financial institution or it can be from retained profits.
i. If the firm is obtaining funds from investors or from a financial institution it has to pay some consideration in the form of return.
ii. Further if the firm uses its retained earning then it should consider opportunity cost.
For example if a firm has a retained profit of Rs.1000 it can invest it and earn interest on it, rather than investing it in a capital expenditure and waiting for year to get return. Thus retained earning can be used to earn more money. The earlier the money is received, the greater the potential for increasing wealth. Thus, to forego the use of money, a firm must get some compensation.
Thus, a firm should undertake an investment proposal only if the present value of the cash flow that the investment generates is greater than the cost of making the investment. The NPV method takes into account the time value of investors’ money and firm retained earnings, it discounts the firm’s cash flows at the firm’s Cost of Capital (COC).
Cost of Capital here indicates the minimum return that must be earned from an investment proposal to satisfy the firm’s investors. Investment proposal with lower returns fail to meet investors’ expectations and therefore decrease firm value, and investment proposal with higher returns increase firm value.
Thus, Net Present Value of an investment proposal is the total of present value of the cash inflows minus Total present value of the cash outflows.
The net present value (NPV) is found by subtracting a project’s initial investment (CFo) from the present value of its cash inflows (CFn) discounted at a rate equal to the firm’s cost of capital (r).
Second Method:
In the first method we try to figure out the value of cash inflow at the end of every year by dividing it with discount factor also referred as cost of capital. In the second method we calculate worth of Re.1 at the end of every year by using discount factor, the outcome of this step is called present value of Re.1, then multiply the PV of Re.1 with cash flow generated in that specific year.
The present value of Re. 1 is computed using the following equation:
Procedure for Calculating Net Present Value:
a. Determine appropriate discount rate, discount rate is the Cost of Capital that indicates the minimum return that must be earned from art investment proposal to satisfy the firm’s investors or lenders.
b. Using cost of capital/discount rate determine present value factors of Re.1.
c. Multiply the cash inflows received from investment proposal during its lifetime with present values. The outcome of this step is called Present Value of Cash flows (PVCF).
d. Calculate the sum of Present Value the Cash flows and deduct initial investment. The outcome of this step is call Net present value (NPV).
Acceptance and Rejection Criteria:
In case of independent investment proposals. If the NPV > 0, then accept. If the NPV < 0, then reject. If the NPV = 0, then depending on the requirement & strategy of the management decision can be taken. In case of mutually exclusive project after making a comparison, investment proposal with a higher NPV (NPV > 0) should be accepted.
II. Profitability Index Method:
Profitability Index Method is an extension of NPV method, NPV method presents the value in absolute measure as it gives the total rupee figure for an investment proposal (Net Present Value of an investment proposal is the total of present value of the cash inflows — Total present value of the cash outflows).
Whereas the profitability index is a relative measure as it gives as the figure as a ratio. In other words, Profitability Index represents the costs and benefits of investing in a particular investment proposal in the form of a ratio, the ratio that is created by comparing the ratio of the present value of future cash flows from a proposal to the initial investment in the proposal.
Procedure for Calculating Profitability Index:
The profitability index can be calculated by dividing the present value of future cash flows expected to be generated from an investment proposal by initial investment of the proposal.
The formula is:
Acceptance and Rejection Criteria:
Profitability index is also referred as benefit-cost ratio and it is also useful in capital rationing since it helps in ranking projects based on their return. In case of independent investment proposals. If the PI > 1, then accept. If the PI < 1, then reject. In case of mutually exclusive project after making a comparison, investment proposal with a higher PI (but it should be >1) should be accepted.
III. Internal Rate of Return Method:
Like net present value method, internal rate of return method also takes into account the time value of money. The internal rate of return (IRR) is the rate of return promised by an investment proposal over its useful life. It is also referred to simply as yield on investment proposal.
Thus, internal rate of return is the rate that equates the present value of an investment proposal with the proposal’s present value of cash inflows. In other words Internal rate of return is the rate at which Total Present value of Cash inflows from the proposal = Initial Investment.
Procedure for Calculating Internal Rate of Return:
One the key difference in NPV and IRR is the way the rate of discount factor/Cost of capital is determined. In case of NPV method the discount factors is based on assumption, whereas in IRR method is identified by the trial and error method. The following are the basic steps involved in calculation of IRR.
Determine IRR Factor:
The first step in finding out the internal rate of return is to compute a discount factor called internal rate of return factor. It is computed by dividing the investment required for the project by net annual cash inflow to be generated by the project.
The formula is given below:
i. Locating discount rate in “present value of table, Re.1 received annually for N years”.
After computing the internal rate of return factor, the next step is to locate this discount factor in “present value of an annuity of Re.1 in “present value of an annuity table”. In order to locate Discount rate in table it is important to consider Life of Proposal or Duration of cash inflow. For example – If a machine has 10 years life, the factor would be found in 10-period line or row.
ii. Computing discount rate and determine PV of cash inflows.
In some cases further it may not be possible to locate accurate discount rate based on IRR factor, therefore we must pick up two discount rates. A higher discount rate and Lower rate. After identifying Lower and Higher discount Rate, We must find out present value of cash flows using Higher and Lower discount rates, then the following formula is applied to calculate internal rate of return-
Note 1- Cash flows means Cashflow before Depreciation after Tax (CFBDAT).
Note 2- The Total of Present Value of Cash flows at Lower discount should be positive. Incase if don’t get a positive value the discount factor should modified, so that we arrive at a Positive total of Present Value of Cash flows.
Acceptance and Rejection Criteria:
If the IRR of an independent investment proposal is greater than or equal to the proposal’s Discount rate (cost of capital), accept the investment proposal. However, if the IRR is less than the proposal’s (cost of capital), reject the investment.
In case of mutual proposal, accept the proposal with greater IRR provided it is greater than the discount rate. The logic of IRR is that never undertake an investment proposal that gives returns less money than that needs to be paid investors/money lenders (cost of capital).
Techniques of Capital Budgeting – 8 Techniques (With Assumptions and Formulas)
Capital expenditures represent long-term commitment in the sense that current investment yields benefits beyond one year in future. As such, the decisions in respect of such expenditures have far reaching effect upon concern’s future earnings and growth. Thus, capital expenditures decisions assume great importance for the future development of the concern. Thus, a sound appraisal method should be used to measure and evaluate the economic worth of a capital expenditure project.
Any appraisal method should satisfy at least the following conditions:
(i) It should serve as a basis for distinguishing between acceptable and rejectable proposals.
(ii) It should provide a basis for ranking the various proposals in order of their desirability.
(iii) It should also help in choosing among alternative proposals.
(iv) It should equally be applicable to any conceivable proposal.
(v) It should recognise the motto that “larger benefits are preferable to smaller ones and early benefits are preferable to latter benefits.”
(vi) It should relate the stream of future savings to the cost of obtaining these benefits.
Taking into account the above points, a number of appraisal methods may be recommended for evaluating the capital expenditure proposals.
The most important and commonly used methods are:
a. Urgency Method
b. Pay-back Period Method
c. Unadjusted Return on Investment Method
d. Present Value Method
e. Net Present Value Method
f. Terminal Value Method
g. Internal Rate of Return Method
h. Benefit-Cost Ratio Method
The methods mentioned at serial number d to h are based on time-value of money and are known as time-adjusted techniques or sophisticated methods.
The above methods will be explained on the assumptions that-
(i) Minimum rate of return (Cost of Capital) or cut-off rate is given,
(ii) Risk and uncertainty are common to all proposals, and
(iii) The financing and dividend decisions are constant.
Again, these methods will help management in taking decisions objectively but they should also exercise their common sense and judgement in taking such decisions.
a. Urgency Method:
There are many situations in the life of a business concern when an ad-hoc decision is needed in respect of a capital expenditure. A decision as a part of well-conceived plan may bring a lot of economic hardships under such a situation. For instance, if a part of machine stops working leading to complete breakdown and disruption in the production, it will be justified to replace it immediately by a new one even without comparing the cost and future profit.
Any decision on capital expenditure on the basis of urgency should be taken only if it is fully warranted and justified by the particular situation arisen in the operating life of the concern.
b. Pay-Back Period Method:
The most commonly used and simple technique for taking decisions on capital expenditure is pay-back period method. It is also sometimes called pay-out or pay-back method. This method describes in terms of period of time the relationship between annual savings (cash inflow) and total amount of capital expenditure (investment). To put it in other way, this method represents the period (normally in number of years) which is required to get back the original cost of investments by annual savings.
Thus, under this method, it is observed on the basis of annual savings as in how many years the total amount of capital expenditure will be recovered. To be more precise, this is simply the investment divided by annual savings.
This period may be calculated by the following formula:
Pay-back Period = NI/OS or NI/Cash Inflow
Hence, NI = Net Investment
OS = Operating Savings
Advantages of Pay-Back Period Method:
(i) It is very easy in calculation and consequently very easy for the line managers to understand.
(ii) If there is likely to be deficiency in cash position or there is a fear of project being obsolete in a very short period, pay-back period may help in gathering information as how rapidly the capital investment may be recovered.
(iii) Sound and effective decisions on capital expenditures may be taken on the basis of pay-back period in case of those industries, where rapid technological changes do take place. Lower the pay-back period in such cases, greater is the margin of safety from the expected loss through obsolescence.
(iv) Where the returns (savings) beyond three to four years are assumed to be uncertain and hence there is no need to recognise them in deciding capital acquisitions, only pay-back period method can be used as a method of evaluating such projects.
(v) It is certainly an improvement over urgency method.
Disadvantages (Limitations) of Pay-Back Period Method:
Although this method has the advantages of simplicity and has been used for many years and is very popular, it suffers from many weaknesses and limitations.
These are:
(i) This method is not an exact measurement of productivity of capital expenditure plan, because it does not attempt to measure the return on investment. Undue emphasis is given to quick and fast recovery of invested fund. Too much emphasis on the ‘liquidity of the investment’ ignoring the ‘profitability of investment’ may not be justified in a number of situations.
(ii) This method does not highlight upon the quantum of income (savings) which could be earned during the whole economic life of investment. In other words, this method does not consider the amount of profit earned on investment after the recovery of cost of investment.
(iii) This method also fails to assign proper weightage to the unevenness of rate of profit of various projects.
(iv) This method also fails to consider the period of time over which an investment is likely to fetch income. In other words, it ignores interest factor which is considered to be a very significant factor in taking sound investment decision.
(v) The most significant limiting factor of this method is that it ignores the ‘time factor’. It is widely now recognised that amount receivable at various future dates should be discounted at present value, otherwise comparative study of all projects cannot be undertaken.
(vi) This method also does not consider the ‘cost of capital’ which is a base for sound investment decisions.
Improvements in Traditional Approach to Pay-Back Period:
Inspite of many weaknesses, pay-back period method is very popular in western countries. On account of this, greater use of this method, some authorities on Accountancy have ventured to bring some improvements in traditional approach to remove some of its defects or weaknesses.
These improvements are discussed under:
1. Discounted Pay-Back Period:
Discounting aspect or interest factor or time value of money has been ignored in the method of pay-back period. This method can be improved or modified to consider the time value of money. When Pay-back period is calculated by taking into account the discounting or interest factor, it is known as Discount Pay-back period.
2. Bail-Out Pay-Back Period:
This method is an improvement over traditional pay-back period in the sense that it considers the salvage value of the projects under evaluation for calculating the pay-back period. This is more useful in the case of such capital expenditure decisions, where risk is a very important factor.
Under this method, the salvage value of the asset over the entire period of life is first estimated. Every year’s savings is accumulated in cumulative form. Each year’s cumulative total of savings is increased by the salvage value of that particular year. The period, when such cumulative savings plus salvage value equal to total cost of investment, is known as Bail-out Pay-back Period.
3. Post Pay-Back Profitability:
The other important limitation of traditional pay-back period is that it neglects the profitability of investment during the excess of economic life period over the pay-back period of that investment. To get rid of this limitation, it is suggested to calculate savings for post pay-back period of the economic life of various projects. If other things remain equal, that project is to be preferred which has highest Post Pay-back period Profits.
For calculating such profit (it is also called surplus savings), the following steps are to be taken:
(i) Find out surplus life in years. This is the excess of actual economic life in years over pay-back period in years.
(ii) If annual savings are even for the entire period, multiply the annual savings by the surplus life in years. This will give total profits or surplus savings for the post pay-back period. If savings are not even, then cumulative totals of savings for each year of surplus life shall be post pay-back period profit.
(iii) It will be better to add the estimated value of scrap in each case to the surplus savings.
(iv) For the sake of clarity in comparison, such surplus savings or Post pay-back profits are converted into index number showing relative importance of each project more precisely.
The formula for such conversion is as under:
4. Pay-Back Reciprocal:
The weakness in traditional pay-back period, that it neglects time factor and does not highlight upon the rate of return, can be removed by calculating the reciprocal of pay-back period.
The formula for calculating pay-back reciprocal is:
Pay-back Reciprocal = 1/Pay-Back Period
When this pay-back reciprocal is converted into percentage, it tends to approach to Time Adjusted Return on Investment (I.R.R.). If, for example, the pay-back period is 4 years, pay-back reciprocal will be 1/4 or in percentage 25 and this 25% is T.A.R.O.I.
However, this method of ranking investment proposals should be used only when:
(i) Annual savings are even for the entire period.
(ii) The economic life of the project is at least twice of the pay-back period.
c. Accounting Rate of Return Method or Unadjusted Return on Investment Method:
This method is also called Accounting Rate of Return Method or Financial Statement Method or Return on Investment (R.O.I.) or Average Rate of Return (A.R.R.) Method. Whatever may be the name of this method, it attempts to measure the rate of return on investment in a project. When initial investment is taken into account in the calculation, it is called R.O.I, and when average investment (capital) is being considered for the purpose of calculation, it is called A.R.R.
The alternative formula for calculating the unadjusted return on investment is:
In both formulae the amount of Operating Savings (OS) is taken to be the average earnings, i.e., total earnings before depreciation for whole period of economic life is divided by the number of years of economic life. The amount of depreciation as represented by NI/n is deducted from operating savings just to provide for depreciation to be created in entire period of economic life of the asset.
As regards the denominator in both formulae, some experts prefer it to be Initial Investment as represented by NI and some prefer it to be Average Investment as represented by NI/2. If there is a scrap value, then cost minus salvage value will be divided by two and to this Salvage Value should be added.
If there is additional working capital required by the project, it should also be added. Normally, a minimum return rate is generally fixed which is known as Rejection criterion. In case of several projects, different projects can be ranked in descending order of the magnitude of actual A.R.R. Thus, projects giving higher rate of return will be preferred.
A comparative study of such return rates in respect of all projects is undertaken and only that project is recommended for approval which yields a comparative higher return rate.
If scrap value is given, formula for calculating average investment will be as under:
Advantages of this Method:
The following advantages are said to accrue from the use of unadjusted rate of return method:
(i) It is widely used because it is easy to understand and simple to calculate like pay-back period.
(ii) It takes into account savings over the entire period of economic life of the investment.
(iii) This method duly recognises the concept of net earnings, i.e., earnings after providing for depreciation on capital asset, which is considered to be a vital factor in the appraisal of a investment proposal.
(iv) This method will distinguish accurately between investments, where the timing of savings is approximately the same.
(v) This method also facilitates the comparison of new product project with that of cost-reducing project or other projects of competitive nature.
Disadvantages or Limitations of this Method:
The unadjusted rate of return method suffers from several weaknesses which are also called limitations.
Some of the weaknesses are as under:
(i) This method may not reveal true and fair view in the case of long-term investments. There is always a fear of over-valuation of the position.
(ii) The principal disadvantage of this method is that it treats a rupee to be received in the future as equal in value to a rupee received today.
(iii) This method also does not take into account life period of the various investments. While average earning is calculated by taking life period into account, investment (whether initial or average) is ascertained without reference to the life period. As a result, average investment or initial investment may remain the same whether investment has a life period of 4 years or 6 years as evident in the example just solved.
(iv) The variants used in the formulas are such that varying interpretations may be assigned to them. This is more true to the average earning and investment.
(v) Another problem is what should be reasonable rate of return. A minimum rate is always fixed and investment yielding a return higher than this minimum is approved. But the determination of this minimum is really a problem, if let it not be an arbitrary one.
d. Present Value Method:
The Present Value (P.V.) Method is one of the Discounted Cash Flow (D.C.F.) or time-adjusted methods. This method recognises that cash inflows and outflows at different time periods differ in value and can be compared only when they are expressed in terms of common denominator, i.e., they are converted to present values.
The following steps are involved in this method:
(i) Determination of cash outflows (initial investments and subsequent outlay) and cash inflows for different periods.
(ii) Determination of discounting rate, i.e., cut off rate. It is generally taken to be equal to cost of capital, because a project must earn at least that much as is paid out on the funds blocked in the project.
(iii) With the help of this discounting rate, present value of cash inflows at different periods may be calculated. For this purposes, Present Value Factor (P.V.F.) is calculated by 1/(1 + i)n or taken from the annuity tables.
(iv) Present value of all cash inflows for different periods are added together. Thus-
P.V. = Cash inflow x P.V.F.
It should be remembered that salvage value and working capital released at the end of project’s life are also considered as cash inflows and are duly discounted to present values.
(v) Cash outflows at zero period of time are not discounted; initial amount is taken as present value of cash outflow. However, cash outflows at subsequent periods are discounted by the same P.V.F.
The present values total of cash inflows should be compared with present values of cash outflows. If the present value of cash inflows are greater than (or equal to) the present value of cash outflows (or initial investment), the project would be accepted. If it is less, then proposal will be rejected.
e. Net Present Value (N.P.V.) Method:
This method is also called Excess Present Value (E.P.V.) Method or Net Gain Method or Investor’s Method and its slightly different version is discounted cash flow method. This is the best method of evaluating the investment proposals and is just a variation of Present Value Method. As such, it is a type of Present Value calculation which is designed to overcome the disadvantages of Internal Rate of Return.
This method is used, when management has already determined a minimum rate of return (cut-off rate) as their policy. All cash flows (cash outflows and cash inflows) are discounted at a given rate and their present values are ascertained. It may be noted that if all Cash Outflows are made in the initial year, their present values will be equal to initial investment outlay.
Present values of cash outflows are then deducted from the present values of cash inflows.
Thus, net present values obtained in the above manner may be equal to zero, more than zero (positive) or less than zero (negative). A project is approved (accepted) only when such present values of Cash Inflows are equal to or more than the present values of Cash Outflows {i.e., initial investment at zero period of time). Thus, N.P.V. should be positive for the approval of a project or it should be equal to zero.
If N.P.V is negative, the project will be treated as worthless and is to be outright rejected. Even N.P.V. method can be used to rank the various proposals which are mutually exclusive. As a general rule, higher the amount of N.P.V. greater worthiness of the project will be. Among the various alternative investment proposals having the same cost, the best one will be one which provides highest N.P.V.
Advantages of this Method:
In addition to advantages mentioned in respect of Present Value and Internal Rate of Return, this method has additional advantages like-
(i) It is much simpler in calculation than internal rate of return. The odds of cumbersome calculation in trial and error procedure are eliminated in this method.
(ii) The desired rate of return fixed by the management does in general represent the rate at which other investment opportunities may be available and hence this method will distinguish more clearly and accurately between alternative investment proposals.
(iii) It is consistent with the objective of maximising owners’ welfare.
Disadvantages or Limitations of this Method:
(i) This method does not indicate the rate of return which is expected to be earned. The determination of desired rate of return proves to be a difficult affair because much line management frequently find at loss to understand this concept.
(ii) Another drawback (and incidentally is applicable to all other methods also) is that this method is static to the extent it freezes the situation at a point of time. Business situations are in reality dynamic and to that extent all calculations may be unrealistic.
(iii) The method may fail to give satisfactory answer when projects under consideration are involving different amounts of investments and with different economic life periods.
f. Terminal Value (T.V.) Method:
This method is based on the assumption that operating savings (cash inflows) of each year is reinvested in another outlet at a certain rate of return from the moment of its receipt till the end of the economic life of the project. However, cash inflows of the last year of the project will not be reinvested. As such, the compounded values of cash inflows should be determined by the following formula-
A = P (1 + i)n, where P = 1
The total sum of compounded cash inflows would be assumed to have been received at the end of the life of the project and hence should be discounted at present values on the basis of discounting rate. The present values of compounded cash inflows should be compared with present values of cash outflows.
If present values of compounded cash inflows are higher than present values of cash outflows (initial outlay) the project should be accepted, otherwise it should be rejected. The management will be indifferent, if both are equal. Like N.P.V., we can also calculate Net Terminal Value (N.T.V.) and if it comes positive, the project should be accepted.
Advantages of this Method:
(i) This method incorporates the assumption about how the cash inflows are reinvested once they are received and thus avoids any influence of the cost of capital on cash inflows.
(ii) It is mathematically easier and makes the evaluation procedure simple.
(iii) It is easier to be understood by those business executives who are not trained in accounting or economics.
(iv) It is more suitable where cash budget is in operation.
Disadvantages or Limitations of this Method:
(i) The most limiting aspect of this method is related to the projection of rates of return at which cash inflows of different years may be reinvested.
(ii) It fails to make comparative evaluation of two or more mutually exclusive proposals.
g. Internal Rate of Return (I.R.R.) Method:
This method is also called Time Adjusted Return on Investment or Discounted Rate of Return (D.R.R.). This method measures the rate of return (time adjusted) which earnings are expected to yield on investments. This method is used when cost of investment and annual savings (cash inflows) are known and unknown rate of earnings duly recognising the time value of rupee is to be calculated.
This rate of return will be a rate of discount at which the net present value of the project is exactly equal to zero. In other words, it is the rate at which present values of annual savings just equal to cost of investment. While using this method, the decision to accept the proposal will be when it is greater than or equal to the cut-off rate (generally cost of capital) and to reject it if the rate (I.R.R.) is less than cut-off rate.
Such rate of return which incidentally coincides with discounting rate can be ascertained in the following manner:
(a) When Savings are Even for All the Years:
When savings are even, the present values of future savings may be found from the following formula-
Since the cost of investment (V), annual savings (a) and number of years (n) for which savings are likely to be generated are known variables, the discounted rate of return or effective rate of return (i) may be found out from the above present value formula.
(b) When Savings are not Even:
Time Adjusted Rate of Return or D.R.R. or I.R.R. may also be found out when savings or cash inflows are uneven. But this can be done only through Trial and Error Method which will be different from one discussed above. Here again the main problem is to find out a rate on which the present value of uneven savings are just equal to the cost of investment.
Thus, I.R.R. or Time Adjusted Rate of Return is a rate in this Case where present values of cash outflows minus present values of cash inflows is equal to zero. For this purpose, the present values of cash inflows are calculated at varying rates. In that process the rate on which present values of cost inflows are closest to the cost of investment is taken to be time adjusted rate of return.
Just to start, the average of the cash inflows of different years may be found. Net Investment should be divided by this average cash inflow. This may be taken as present value factor.
Thus, total of such present values should be compared with the cost of investment. If the total of present values is higher than the cost of investment, then further interpolation is done at a higher rate. On the other hand, if the total of present values is less than the cost of investment, then further interpolation is carried on at lower rate. By following such trial and error, the actual I.R.R. may be ascertained.
However, the exact rate may be interpolated as under:
Advantages of this Method:
Undoubtedly, this method provides more and precise information regarding profitability. It is a much more precise technique of ranking investment proposal than pay-back period and Return on Investment (unadjusted).
Usually, the advantages of this method are:
(i) Since the timing of savings is taken into account, significant factors which cannot be handled adequately by the unadjusted return of invested method, may be included in the analysis of this method.
(ii) The internal rate of return is more realistic and is consistent with the rate of interest paid on borrowings, rate of return on debentures or the yield from shares, etc. In the case of unadjusted rate of return if average investment is used as the denominator, the rate of return will be overstated. If the initial outlay is used as denominator, the rate of return will be understated. This is not the case with I.R.R.
(iii) The impact of time on investment will be lesser in the case of time adjusted rate of return than in the case of unadjusted return on investment. This improves the quality of estimate in the sense that uncertainty would be reduced to minimum if the distance is greater.
Disadvantages or Limitations of this Method:
From the point of view of practical use of this method, a number of weaknesses are pointed out and these are:
(i) A number of refined considerations taken into account in the calculation under this method may bring uncertainty in themselves.
(ii) Selection of interest or discounted rate also poses a number of practical difficulties.
(iii) This method has also the disadvantage of not making distinction between alternative investments with complete accuracy because of assumption (implicit in calculation) that income cash can be invested at the rate indicated by internal rate of return.
Comparison of N.P.V. and I.R.R:
We have just explained the various methods based on time adjusted value. Let us now compare few of them. N.P.V. and I.R.R. (to take first) are similar in certain respects.
But they also differ in other respects as mentioned below:
(i) Though both methods proceed on the presumption that cash inflows can be reinvested reinvestment under N.R.V. is taken to be at cut-off rate (cost of capital) and under I.R.R. it is taken to be reinvested at internal rate of return itself.
(ii) Under N.P.V. interest rate is taken as known factor but I.R.R. method takes it as an unknown factor.
(iii) N.P.V. method attempts to find out the amount which can be invested in a project so that its expected earnings will exactly suffice to repay this amount with interest at market rate. But I.R.R. method tries to find out the maximum rate of interest at which amount invested in a project could be repaid out of cash inflows arising out of that project.
(iv) Though both methods may give similar results under some situations, they may provide contradictory results under other situations as explained below.
Cases of Similar Results under Both the Methods:
Under the following cases, both N.P.V. and I.R.R. will give the same result (i.e., acceptance or rejection) in respect of an investment proposal:
(i) Where proposals are independent i.e., investment proposals the acceptance of which does not preclude the acceptance of other, so that all profitable proposals can be accepted and there are no constraints in accepting all profitable proposals.
(ii) Where proposals involve conventional cash flows, i.e., proposal in which the cash flow pattern is such that an initial investment (i.e., cash outflow at zero period of time) is followed by a series of cash inflows. Thus, in the case of such proposals, cash outflows are confined to the initial period.
The reason for similar results under the above cases by both the methods is very simple. In the case of N.P.V. a proposal is acceptable only when N.P.V. is positive. This will be true only when actual return on investment is higher than the cut-off rate. In the case of I.R.R., a proposal is acceptable only, if its I.R.R., is higher than cut-off rate. As such a proposal having positive N.P.V. will also have an I.R.R. higher than the cut-off rate.
Cases of Different Results under Both the Methods:
There will be certain situations, where both N.P.V. and I.R.R. may give contradictory results, i.e., a proposal may be acceptable as per N.P.V., while I.R.R. may favour another proposal. This is particularly true when investment proposals are mutually exclusive proposals, i.e., proposal acceptance of which may preclude the acceptance of other.
The difference in results may be due to any one or more of the following reasons:
(i) Initial investment in different projects may differ, i.e., size-disparity,
(ii) Different projects may have different or unequal economic lives, and
(iii) The pattern of cash flows may differ from project to project.
One important question arising in the above situation is – Which method should be adopted for having better result?
The answer will differ from point to point listed above and may be generalised as under:
(i) When initial investment differs from project to project, N.P.V. method would give better result than I.R.R. because N.P.V. is more consistent with the objective of maximising shareholder’s wealth. Of all the mutually exclusive projects a project having highest positive N PV will have the most beneficial effect on shareholders’ wealth. This is because a proposal having highest N.P.V. will cause the share price and shareholders’ fund to increase more than what will be possible with any of the other projects.
The above problem can also be resolved by modifying the I.R.R. on an incremental type of analysis. According to this approach, in case of two mutually exclusive projects requiring different initial investments, the I.R.R. of incremental investment of the proposal requiring higher initial investment is calculated. If the I.R.R. of the incremental cash flows exceeds the required rate of return, the proposal having greater non-discounted cash flows should be accepted.
(ii) Where projects have different (unequal) expected lives, the conflict in the results by the two methods can be resolved by comparing the projects over the same period of time. As such, a project having shorter life should be assumed to have been invested in a similar other shorter life project after expiry.
(iii) Where projects have different pattern of cash flows, the problem can be resolved by preferring N.P.V. to I.R.R. as suggested in (i) above.
h. Benefit-Cost Ratio Method (Profitability Index):
This method, also based on time adjusted techniques, is also called Profitability Index’ (P.I.) or Desirability Factor (D.F.). It is basically a refinement of the N.P.V. Method. This ratio (B/C) or (P.I.) is expressed either in per rupee or in percentage. Again, this ratio may be between Present Values (P.V.) of cash inflows and Present Values of cash outflows (Cost of Investment) or it may be between Excess Present Values (E.P.V.) and cost. Since it is ratio, therefore it happens to be a relative measure and may be used in evaluating the proposals requiring different initial investment (Cost).
This ratio may be calculated as under:
It may be observed that on the basis of B/C Ratio (P.I.), a project will qualify for acceptance only when its P.I. exceeds one (or hundred in case it is expressed in percentage). Higher comes this ratio, more desirable will be the project. This method can also be used for ranking the various proposals. A project assuming the highest rank will be most acceptable.
Like all other discounted cash flow techniques (i.e., P.V., N.P.V., I.R.R. and T.V.), this method is also conceptually a sound method of evaluating investment proposals.
The merits of this method are:
(i) It is superior to N.P.V. method in the sense that it evaluates the worth of projects in terms of their relative magnitudes.
(ii) It can also be used to choose between mutually exclusive projects by calculating incremental benefit cost ratio.
(iii) It gives due consideration to the time value of money and cost involved in each project.
Disadvantages or Limitations of this Method:
(i) It is more difficult to understand and involves more calculations than the traditional methods (but less than I.R.R. method).
(ii) In some cases of mutually exclusive nature, N.P.V method would be superior to this method.
Comparison of N.P.V. and P.I.:
These two methods are closely related to each other and hence provide the same results in most of the situations. A proposal is accepted if P.I. is more than one (or 100) and it will have such value only when N.P.V is positive (which happens to be the accepted criterion under N.P.V.). Similarly, P.I. will be less than one (or 100) when investment proposal has negative N.P.V. (and in both methods this is the criterion for rejection).
However, these methods may provide conflicting results when proposals are mutually exclusive and are to be evaluated by ranking. Again, N.P.V. method should be preferred to P.I., if the objective is to select that project which adds the most to the shareholders’ wealth.