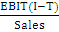The following points highlight the top seven investment appraisal techniques. The techniques are: 1. Payback Period Method 2. Accounting Rate of Return Method 3. Net Present Value Method 4. Internal Rate of Return Method 5. Profitability Index Method 6. Discounted Payback Period Method 7. Terminal Value Method.
Technique # 1. Payback Period Method:
The payback period is usually expressed in years, which it takes the cash inflows from a capital investment project to equal the cash outflows. The method recognizes the recovery of original capital invested in a project. At payback period the cash inflows from a project will be equal to the project’s cash outflows.
This method specifies the recovery time, by accumulation of the cash inflows (inclusive of depreciation) year by year until the cash inflows equal to the amount of the original investment. The length of time this process takes gives the ‘pay-back period’ for the project. In simple terms it can be defined as the number of years required to recover the cost of the investment.
In case of capital rationing situations, a company is compelled to invest in projects having shortest payback period. When deciding between two or more competing projects the usual decision is to accept the one with the shortest payback.
ADVERTISEMENTS:
Payback is commonly used as a first screening method. It is a rough measure of liquidity and rate of profitability. This method is simple to understand and easy to apply and it is used as an initial screening technique. This method recognizes the recovery of the original capital invested in a project.
Merits:
(a) It is simple to apply, easy to understand and of particular importance to business which lack the appropriate skills necessary for more sophisticated techniques.
(b) In case of capital rationing, a company is compelled to invest in projects having shortest payback period.
ADVERTISEMENTS:
(c) This method is most suitable when the future is very uncertain. The shorter the payback period, the less risky is the project. Therefore, it can be considered as an indicator of risk.
(d) This method gives an indication to the prospective investors specifying when their funds are likely to be repaid.
(f) Ranking projects according to their ability to repay quickly may be useful to firms when experiencing liquidity constraints. They will need to exercise careful control over cash requirements.
(e) It does not involve assumptions about future interest rates.
ADVERTISEMENTS:
Demerits:
(a) It does not indicate whether an investment should be accepted or rejected, unless the payback period is compared with an arbitrary managerial target.
(b) The method ignores cash generation beyond the payback period and this can be seen more a measure of liquidity than of profitability.
(c) It fails to take into account the timing of returns and the cost of capital. It fails to consider the whole life time of a project. It is based on a negative approach and gives reduced importance to the going concern concept and stresses on the return of capital invested rather than on the profits occurring from the venture.
ADVERTISEMENTS:
(d) The traditional payback approach does not consider the salvage value of an investment. It fails to determine the payback period required in order to recover the initial outlay if things go wrong. The bailout payback method concentrates on this abandonment alternative.
(e) This method makes no attempt to measure a percentage return on the capital invested and is often used in conjunction with other methods.
(f) The projects with long payback periods are characteristically those involved in long-term planning, and which determine an enterprise’s future. However, they may not yield their highest returns for a number of years and the result is that the payback method is biased against the very investments that are most important to long-term.
Technique # 2. Accounting Rate of Return Method:
The accounting rate of return is also known as ‘return on investment’ or ‘return on capital employed’ method employing the normal accounting technique to measure the increase in profit expected to result from an investment by expressing the net accounting profit arising from the investment as a percentage of that capital investment.
ADVERTISEMENTS:
The method does not take into consideration all the years involved in the life of the project. In this method, most often the following formula is applied to arrive at the accounting rate of return.
Sometimes, initial investment is used in place of average investment. Of the various accounting rates of return on different alternative proposals, the one having highest rate of return is taken to be the best investment proposal. For example, in three alternative proposals A, B and C with expected accounting rates of return of 10%, 20% and 18% respectively.
ADVERTISEMENTS:
Projects will be selected in order of B, C and A. If the prevailing rates of interest is taken to be 15% p.a., only proposals B and C will qualify for consideration and in that order.
Merits:
(a) It is easy to calculate because it makes use of readily available accounting information.
(b) It is not concerned with cashflows but rather based upon profits which are reported in annual accounts and sent to shareholders.
ADVERTISEMENTS:
(c) Unlike payback period method, this method does take into consideration all the years involved in the life of a project.
(d) Where a number of capital investment proposals are being considered, a quick decision can be taken by use of ranking the investment proposals.
(e) If high profits are required, this is certainly a way of achieving them.
Demerits:
(a) It does not take into accounting time value of money.
(b) It fails to measure properly the rates of return on a project even if the cashflows are even over the project life.
ADVERTISEMENTS:
(c) It uses the straight line method of depreciation. Once a change in method of depreciation takes place, the method will not be easy to use and will not work practically.
(d) This method fails to distinguish the size of investment required for individual projects. Competing investment proposals with the same accounting rate of return may require different amounts of investment.
(e) It is biased against short-term projects in the same way that payback is biased against longer- term ones.
(f) Several concepts of investment are used for working out accounting rates of return. Thus there is no full agreement on the proper measure of the term investment. Thus different managers have different meanings when they refer to accounting rate of return.
(g) The accounting rates of return does not indicate whether an investment should be accepted or rejected, unless the rates of return is compared with the arbitrary management target.
Illustration 1:
Consider the following investment opportunity:
A machine is available for purchase at a cost of Rs. 80,000.
We expect it to have a life of five years and to have a scrap value of Rs. 10,000 at the end of the five year period.
We have estimated that it will generate additional profits over its life as follows:
These estimates are of profits before depreciation. You are required to calculate the return on capital employed.
Solution:
Total profit before depreciation over the life of the machine = Rs. 1,10,000
... Average profit p.a. = Rs. 1,10,000/5 years = Rs. 22,000
Total depreciation over the life of the machine (Rs. 80,000 – Rs. 10,000) = Rs. 70,000
... Average depreciation p.a. = Rs. 70,000/5 years = Rs. 14,000
... Average annual profit after depreciation = Rs. 22,000 – Rs. 14,000 = Rs. 8,000
Original investment required = 80,000
... Accounting rate of return = (Rs. 8,000/Rs. 80,000) x 100 = 10%
Average investment = (Rs. 80,000 + Rs. 10,000)/2 = Rs. 45,000
Accounting rate of return = (Rs. 8,000/Rs. 45,000) x 100 = 17.78%
Technique # 3. Net Present Value Method:
The objective of the firm is to create wealth by using existing and future resources to produce goods and services. To create wealth, inflows must exceed the present value of all anticipated cash outflows. Net present value is obtained by discounting all cash outflows and inflows attributable to a capital investment project by a chosen percentage e.g., the entity’s weighted average cost of capital.
The method discounts the net cash flows from the investment by the minimum required rate of return, and deducts the initial investment to give the yield from the funds invested. If yield is positive the project is acceptable. If it is negative the project in unable to pay for itself and is thus unacceptable. The exercise involved in calculating the present value is known as ‘discounting and the factors by which we have multiplied the cash flows are known as the ‘discount factors’.
The discount factor is given by the following expression:
1/(1 + r)n
Where, r = Rate of interest p.a.
n = number of years over which we are discounting.
Discounted cashflow is an evaluation of the future net cashflows generated by a capital project, by discounting them to their present day value. The method is considered better for evaluation of investment proposal as this method takes into account the time value of money as well as, the stream of cash flows over the whole life of the project.
One of the main disadvantages of both payback and accounting rates of return methods is that they ignore the fact that money has time value. The discounting technique converts cash inflows and outflows for different years into their respective values at the same point of time, allows for the time value of money. This method is particularly useful for the selection of mutually exclusive projects i.e., acceptance of one project amounts to rejection of the other project.
Merits:
(a) It is based on the assumption that cashflows, and hence dividends, determine shareholders’ wealth.
(b) Cashflows are subjective than profits.
(c) It recognizes the time value of money.
(d) It considers the total benefits arising out of proposals over its life time.
(e) The future discount rate normally varies due to longer time span. This rate can be applied in calculating the NPV by altering the denominator.
(f) This method is particularly useful for the selection of mutually exclusive projects. (In mutually exclusive projects, acceptance of one project tantamount to rejection of the other project).
(g) This method of project selection is instrumental in achieving the financial objective, i.e., maximization of the shareholders wealth.
Demerits:
(a) It is difficult to calculate as well as understand it as compared to accounting rate of return method or payback period method.
(b) Calculation of the desired rates of return presents serious problems. Generally cost of capital is the basis of determining the desired rate. The calculation of cost of capital is itself complicated. Moreover, desired rates of return will vary from year to year.
(c) This method is an absolute measure. When two projects are being considered, this method will favour the project which has higher NPV.
(d) This method may not give satisfactory results where two projects having different effective lives are being compared. Normally, the project with shorter economic life is preferred, if other things are equal. This method does not attach importance to the shorter economic life of the project.
(e) This method emphasizes the comparison of net present value and disregards the initial investment involved. Thus, this method may not give dependable results.
Adjusted Present Value:
In the evaluation of capital budgeting proposals, the first step is to estimate the expected cash outflow and inflow of the project. Such estimates are made over economic life of the project and present values of future cashflows are reckoned. While calculation of present values of the future cashflows, otherwise called discounted cashflows, weighted average cost of capital (WACC) is considered as a rate for discounting the cashflows.
In NPV method, cashflows are discounted at WACC rate, and if the present value of cash inflow is higher than the present value of cash outflow, the project can be accepted. The rate of discounted return in the project with the initial outlay is calculated. Under IRR method this rate is the IRR of the project and it is then compared with WACC figure. If WACC of the project is lower than IRR, the project is accepted and vice versa.
Under adjusted present value (APV) approach, the project is splited into various strategic components. The cashflow estimates of the project are first discounted at the cost of equity, and a base-case present value is arrived at as if the project is all-equity financed. After that, the financial side effects are analyzed one by one and duly valued.
For example, if the debt is proposed to be used as a component of capital, then positive impact of tax shield is added to the base-case present values. Likewise, different aspects in cost of financing like capital investment subsidy, flotation costs of public issue/rights issue, administrative cost of equity/debt funds are analyzed separately and a composite position arrived at.
The APV method is considered improvement over WACC method for the reason that by splitting the overall decision into logical pieces and attributing financial values to it, aid the management in correct valuation of the project’s viability. But this approach lays more emphasis on financial risk ignoring the business risk.
Under WACC approach, all flows are post-tax and the discount rate is also post-tax. Thus the benefit of tax shield will get discounted at the WACC. On the other hand, under APV approach, the tax shields are discounted back at the cost of debt.
Technique # 4. Internal Rate of Return Method:
Internal rate of return (IRR) is a percentage discount rate used in capital investment appraisals which brings the cost of a project and its future cash inflows into equality. It is the rate of return which equates the present value of anticipated net cash flows with the initial outlay. The IRR is also defined as the rate at which the net present value is zero.
The rate for computing IRR depends on bank lending rate or opportunity cost of funds to invest which is often called as personal discounting rate or accounting rate. The test of profitability of a project is the relationship between the IRR (96) of the project and the minimum acceptable rate of return (96).
The IRR can be stated in form of a ratio as shown below:
Cash Inflows / Cash Outflows = 1
P.V. of Cash Inflows – P.V. of Cash Outflows = Zero
The IRR is to be obtained by trial and error method to ascertain the discount rate at which the present values of total cash inflows will be equal to the present values of total cash outflows.
If the cash inflow is not uniform, then IRR will have to be calculated by trial and error method. In order to have an approximate idea about such discounting rate, it will be better to find out the ‘factor’. The factor reflects the same relationship of investment and cash inflows as in case of payback calculations.
F = I/C
Where, F = Factor to be located
I = Original Investment
C = Average cash inflow per year
In appraising the investment proposals, IRR is compared with the desired rate of return or weighted average cost of capital, to ascertain whether the project can be accepted or not. IRR is also called as ‘cut off rate’ for accepting the investment proposals.
Merits:
(a) It considers the time value of money.
(b) It takes into account the total cash inflows and cash outflows.
(c) It is easier to understand. For example, if told that IRR of an investment is 20% as against the desired return on an investment is Rs. 15,396.
Demerits:
(a) It does not use the concept of desired rate of return, whereas it provides the rate of return which is indicative of the profitability of investment proposal.
(b) It involves tedious calculations, based on trial and error method.
(c) It produces multiple rates which can be confusing.
(d) Projects selected based on higher IRR may not be profitable.
(e) Unless the life of the project can be accurately estimated, assessment of cashflows cannot be correctly made.
(f) Single discount rate ignores the varying future interest rates.
Relative Ranking of Projects: IRR vs. NPV:
The relative ranking of projects, using the different DCF methods will be considered initially in simple accept/reject situations. This will be extended later to a detailed assessment of situations where a choice has to be made between two or more alternatives.
In simple accept/reject situations a firm is able to implement all projects showing a return at or above the firms cost of capital. Both NPV and IRR would appear to be equally valid in the sense that they will both lead to accept or reject the same projects.
Using NPV, all projects with a positive net present value, when discounted at the firm’s cost of capital, will be accepted. Using IRR all projects which yield an internal rate of return in excess of the firms cost of capital will be chosen. Although IRR and NPV lead to the same conclusion regarding project acceptability, the ranking of a set of projects obtained from IRR does not necessarily agree with that produced using NPV.
Since, in the latter case, the ranking may vary according to particular discount rate used. Argument about the merits of the relative ranking in simple accept/reject situations is thus concerned with the question of value. It is argued that the IRR measures only the quality of the investment while NPV takes into account both the quality and the scale.
This is because the IRR provides a relative measure of value (% IRR) while the NPV provides an absolute measure (Rs. surplus). The IRR would rank, for example, a 100% return on an investment of Re. 1 considerably higher than a 20% return on an investment of Rs. 10 lakhs, whereas the reserve would be true using NPV (as long as the cost of capital is below 20%).
While one project may have a higher rate of profit per unit of capital invested than another, if it has fewer units of capital invested in it, it may make a smaller contribution to the wealth of the firm. Thus if the objective is to maximize the firms wealth, then the ranking of project NPVs provides the correct measure.
If the objective is to maximize the rate of profitability per unit of capital invested, then IRR would provide the correct ranking of projects, but this objective could be achieved by rejecting all but the most highly profitable projects.
This is clearly unrealistic and, therefore, one would conclude that NPV ranking is correct and IRR unsatisfactory as a measure of relative project value. When two investment proposals are mutually exclusive, both methods will give contradictory results. When two mutually exclusive projects are not expected to have the same life, NPV and IRR methods will give conflicting ranking.
Illustration 2:
If a choice has to be made between Project A and Project B because they are operationally mutually exclusive, the project chosen will depend upon the appraisal method used, because conflicting ranking will occur.
In the above illustration, Project B would be preferred based on NPV method, despite offering a lower percentage return on average, it involves investment of an extra Rs. 11,000 – the return on which is sufficient to generate a further profit surplus (i.e., an increase in the NPV) when discounted at 10%.
Differential cashflows of Project A and Project B
Year O Differential investment = (Rs. 11,000)
Year 1-5 Differential cash inflow = Rs. 3,000 p.a.
IRR = 11%
NPV (at 10%) = Rs. 370 (i.e. Rs. 5,320 – Rs. 4,950)
Analysis:
Using IRR, Project A would be chosen because it provides a differential return in excess of the minimum required return. But with the simple observation of IRR between two projects, Project A will be selected because of its higher IRR of 23%.
Multiple Internal Rates of Return:
In some projects there will be initial cash outflow followed by cash inflow. In the middle of the project life there would be another major cash outflow which may result in getting more than one IRR. This situation is called ‘multiple internal rate of returns’. This is shown in figure 31.1 (doubt)
When multiple IRRs arises, the capital project will be selected only when its cost of capital is below the multiple IRRs.
Modified Internal Rate of Return (MIRR):
The MIRR is a refined method of calculating IRR. The MIRR overcomes the weaknesses of IRR. MIRR correctly assumes the reinvestment at the project’s cost of capital and eliminates the problem of getting multiple IRRs.
The steps in calculating MIRR are as follows:
(a) Estimate all the cash flows as in IRR.
(b) Future value of all cash inflows are calculated to the terminal year of the project life.
(c) Determine the discount rate that causes the future value of all cash inflows determined in step (b), to be equal to the firm’s investment at time zero. Such discount rate obtained is called MIRR.
The computation of MIRR is not widely used in practice. IRR is more popularly adopted in project investment decisions.
Technique # 5. Profitability Index Method:
It is a method of assessing capital expenditure opportunities in the profitability index. The profitability index (PI) is the present value of an anticipated future cash inflows divided by the initial outlay.
The only difference between the net present value method and profitability index method is that when using the NPV technique the initial outlay is deducted from the present value of anticipated cash inflows, whereas with the profitability index approach the initial outlay is used as a divisor.
In general terms, a project is acceptable if its profitability index value is greater than 1. Clearly, a project offering a profitability index greater than 1 must also offer a net present value which is positive. When more than one project proposals are evaluated, for selection of one among them, the project with higher profitability index will be selected. Mathematically, PI (profitability index) can be expressed as follows:
Profitability Index (PI) = Present Value of Cash Inflows/Present Value of Cash Outlay
This method is also called ‘cost-benefit ratio ‘or ‘desirability ratio method.
Limitations:
(a) Profitability index cannot be used in capital rationing problems where projects are indivisible. Once a single large project with high NPV is selected, the possibility of accepting several small projects which together may have higher NPV than the single project, is excluded.
(b) Sometimes the project with lower profitability index may have to be selected if it generates cashflows in the earlier years, which can be used for setting up of another project to increase the overall NPV.
Illustration 3:
Analysis:
According to the NPV method, Project A would be preferred, whereas according to profitability index Project B would be preferred. Although PI method is based on NPV, it is a better evaluation technique than NPV in a situation of capital rationing. For example two projects may have the same NPV of Rs. 10,000 but Project A requires initial outlay of Rs. 1,00,000 whereas B only Rs. 50,000. Project B would be preferred as per the yard stick of PI method.
Technique # 6. Discounted Payback Period Method:
In this method the cashflows involved in a project are discounted back to present value terms as discussed above. The cash inflows are then directly compared to the original investment in order to identify the period taken to payback the original investment in present values terms.
This method overcomes one of the main objections to the original payback method, in that it now fully allows for the timing of the cashflows, but it still does not take into account those cashflows which occur subsequent to the payback period and which may be substantial.
The method is a variation of payback period method, which can be used if DCF methods are employed. This is calculated in much the same way as the payback, except that the cashflows accumulated are the base year value cashflows which have been discounted at the discount rate used in the NPV method (i.e., the required return on investment).
Thus, in addition to the recovery of cash investment, the cost of financing the investment during the time that part of the investment remains unrecovered is also provided for. It thus, unlike the ordinary payback method, ensures the achievement of at least the minimum required return, as long as nothing untoward happens after the payback period.
Technique # 7. Terminal Value Method:
Under this method it is assumed that each cashflow is reinvested in another project at a predetermined rate of interest. It is also assumed that each cash inflow is reinvested elsewhere immediately until the termination of the project. If the present value of the sum total of the compounded reinvested cashflows is greater than the present value of the outflows the proposed project is accepted otherwise not.
Merits:
The merits of the terminal value method are summarized below:
(a) This method has the advantage of the cash inflows being reinvested once they are received.
(b) It is mathematically easier to compute as compared to IRR.
(c) It is easier to understand.
(d) It is better suited to cash budgeting requirement.
However, the major problem of this method lies in projecting the future rates of interest at which the cash inflows will be reinvested.
Illustration 4:
Original outlay: Rs. 8,000
Life of the project: 3 years
Cash inflows: Rs. 4,000 p.a. for 3 years
Cost of capital: 10% p.a.
Expected interest rates at which the cash inflows will be reinvested:
Solution:
First of all, it is necessary to find out the total compounded sum which will be discounted back to the present value.
Now, we have to find out the present value of Rs. 12,984 by applying the discount rate of 10%.
12,984/(1.10)3 = 12,984 X 0.7513* = 9,755
(‘0.7513 being the P.V. of Re. 1 received after 3 years.)
Here, since the present value of reinvested cashflows i.e., Rs. 9,755 is greater than the original cash outlay of Rs. 8,000, the project would be accepted under the terminal value criterion.
Assumptions in Use of DCF Techniques:
In use of discounted cashflow techniques the following assumptions should be given consideration:
(a) The discount rate is constant over the life of the investment.
(b) All cashflows can be predicted with certainty so that a risk premium need not be added to the discount rate in order to compensate for risk.
(c) In project appraisal, managers work with uncertain future events and estimated cash flows expected to occur in future years. This involves a substantial amount of estimation which in practical terms, means that spurious accuracy is something which needs to be avoided.
(d) The discount figures used can be calculated with great accuracy but when they are applied to these future estimated cashflows, the resultant calculation is only as accurate as the cashflows estimates.
(e) In many companies there is a tendency to produce discounted cashflow computation with several decimal places on each of the present values. This creates a totally fallacious appearance of accuracy in the evaluation process.
(f) To enable convenient calculations to be performed, it is normal practice in capital project evaluations to assume that all cashflows take place at the end of the year. The initial cash outflows or investment in a project is assumed to take place now. The cashflows which go out now are taken to be at Year 0. The concept of Year 0 does not mean a year in general terms, but a point in time, i.e., today. Year 1 cashflows are assumed to take place at the end of the first year. The second year cashflows occurring at the end of the Year 2 and similarly for subsequent years.
(g) In appraising long-term projects, it is normal to use an arbitrary horizon period of 10 to 15 years. Firms do not consider cashflows beyond the horizon even if they expect the project to last longer.