Top 2 Cash Management Models (With Diagram)

The following points highlight the top two cash management models. They are: 1. Baumol’s EOQ Model of Cash Management 2. Miller-Orr Cash Management Model.

1. Baumol’s EOQ Model of Cash Management:

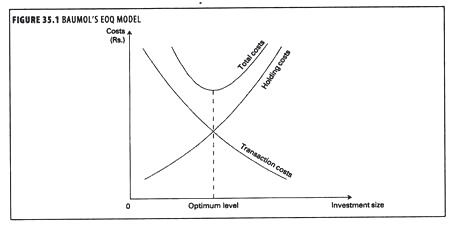
William J. Baumol (1952) suggested that cash may be managed in the same way as any other inventory and that the inventory model could reasonably reflect the cost – volume relationships as well as the cash flows. In this way, the economic order quantity (EOQ) model of inventory management could be applied to cash management. It provides a useful conceptual foundation for the cash management problem.

In the model, the carrying cost of holding cash-namely the interest forgone on marketable securities is balanced against the fixed cost of transferring marketable securities to cash, or vice- versa. The Baumol model finds a correct balance by combining holding cost and transaction costs, so as to minimize the total cost of holding cash.

The optimum level of cash balance is found to be:

Where,

C = Optimum level of cash balance

A = Annual cash payments estimated

T = Cost per transaction of purchase or sale of marketable securities

I = Interest on marketable securities p.a. (i.e., carrying cost per rupee of cash)

According to the model, optimum cash level is that level of cash where the carrying costs and transaction costs are the minimum. The carrying costs refers to the cost of holding cash i.e. interest forgone on marketable securities. The transaction cost refers to the cost involved in getting the marketable securities converted into cash and vice versa.

Assumptions:

The Baumol’s model holds good if the following assumptions are fulfilled:

(a) The rate of cash usage is constant and known with certainty. The model has limited use in times of uncertainty and firms whose cash flows are discontinuous or bumpy.

(b) The surplus cash is invested into marketable securities and those securities are again disposed of to convert them again into cash. Such purchase and sale transactions involve certain costs like clerical, brokerage, registration and other costs. The cost to be incurred for each such transaction is assumed to be constant/fixed. In practice, it would be difficult to calculate the exact transaction cost.

(c) By holding cash balance, the firm is would incur the opportunity cost of interest forgone by not investing in marketable securities. Such holding cost per annum is assumed to be constant.

(d) The short-term marketable securities can be freely bought and sold. Existence of free market for marketable securities is a prerequisite of the Baumol model.

Limitations:

The important limitations in Baumol’s model are as follows:

(i) The model can be applied only when the payments position can be reasonably assessed.

(ii) Degree of uncertainty is high in predicting the cash flow transactions.

(iii) The model merely suggests only the optimal balance under a set of assumptions. But in actual situation it may not hold good.

Nevertheless it does offer a conceptual framework and can be used with caution as a benchmark.

Illustration 1:

The outgoings of Gemini Ltd. are estimated to be Rs. 5,00,000 per annum, spread evenly throughout the year. The money on deposit earns 12% p.a. more than money in a current account. The switching costs per transaction is Rs. 150. Calculate the optimum amount to be transferred.

Solution:

According to Baumol, the optimum amount to be transferred each time is ascertained as follows:

Where,

C = Optimum transaction size

A = Estimate cash outgoings per annum Le. Rs. 5,00,000

T = Cost per transaction Le. Rs. 150

I = Interest rate on fixed deposit Le. 12% p.a.

Number of transactions p.a. = Rs. 5,00,000/Rs. 35,000 = 14 transactions

Average balance in the short notice account = Rs. 35,000/2 = Rs. 17,500

Aggregate of fixed cost = 14 transactions x Rs. 150 = Rs. 2,100

Illustration 2:

ABC Ltd. has estimated that use of Rs. 24 lakhs of cash during the next budgeted year. It intends to hold cash in a commercial bank which pay interest @ 10% p.a. For each withdrawal, the company incurs expenditure of Rs. 150. What is the optimal size for each withdrawal?

Solution:

Each time the firm will withdraw Rs. 85,000 from the bank deposit. After spending all the amount of Rs. 85,000, again the company will withdraw a similar amount and so on.

Illustration 3:

Tarus Ltd. has an estimated cash payments of Rs. 8,00,000 for a one month period and the payments are expected to steady over the period. The fixed cost per transaction is Rs. 250 and the interest rate on marketable securities is 12% p.a. Calculate the optimum transaction size.

Solution:

The optimum transaction size will be calculated as under:

Where,

A = Estimated monthly cash payments i.e. Rs. 8,00,000

T = Cost per transaction i.e. Rs. 250

I = Interest per annum i.e. 12% p.a. (For one month, the rate of interest is 196 or 0.01)

Optimum transaction size = Rs. 2,00,000

Average cash balance = Rs. 2,00,000/2 = Rs. 1,00,000

Number of transactions = Rs. 8,00,000/Rs. 2,00,000 = 4 transactions

2. Miller-Orr Cash Management Model:

Miller and Orr model (1966) assumes that the cashflow of the firm is assumed to be stochastic, i.e. different amounts of cash payments are made on different points of time. It is assumed that the movements in cash balance occur randomly. Miller and Orr suggested a model with control limits, which sets control points for time and size of transfers between an Investment Account and Cash Account.

The model asserts that transfer money into or out of the account to return the balance to a predetermined ‘normal point whenever the actual balance went outside a lower or upper limit.

The lower limit would be set by management, and the upper limit and return points by way of formulae which assume that cash inflows and outflows are random, their dispersion usually being assumed to repeat a pattern exhibited in the past.

The model specifies the following two control limits:

h = Upper control limit, beyond the cash balance should not be carried.

0 = Lower control limit, sets the lower limit of cash balance, i.e. the firm should maintain cash resources atleast to the extent of lower limit.

z = Return point for cash balance

This is represented in figure 4:

The Miller-Orr model, will work as follows:

(i) When cash balance touched the upper control limit (h), securities are bought to the extent of Rs. (h-z).

(ii) Then the new cash balance is z.

(iii) When cash balance touches lower control limit (o), marketable securities to the extent of Rs. (z-o) will be sold.

(iv) Then the new cash balance again return to point z.

Assumptions:

The basic assumptions of the model are:

(a) The major assumption with this model is that there is no underlying trend in cash balance over time.

(b) The optimal values of ‘h’ and ‘z’ depend not only on opportunity costs, but also on the degree of likely fluctuations in cash balances.

The model can be used in times of uncertainty and random cash flows. It is based on the principle that control limits can be set which when reached trigger off a transaction. The control limits are based on the day-to-day variability in cash flows and the fixed costs of buying and selling government securities.

Spread Between the Control Limits:

The higher the variability in cash flows and transaction cost, the wider and higher the control limits will be. Conversely, the higher the interest rate, the lower and closer they will become. Within the control limits, the cash balance fluctuates unpredictably.

When it hits an upper or lower limit, action is taken by buying or selling securities to restore the balance to its normal level within the control points. In applying the model one must set the lower limit for the cash balance. This could be zero or some minimum safety margin above zero.

Illustration 5:

Solution:

Upper Limit = Spread + Lower Limit

= 7,400+1,000 = Rs. 8,400

Return Point = Lower Limit + (1/3 x Spread)

= 1,000 + (1/3 x 7,400) = 1,000 + 2,467 = Rs. 3,467

Illustration 6:

Interest rate per day/annum = 0.3%/10.95%

Transaction cost per sale = Rs.20

Variance of cash flows per day/annum = Rs. 3,000/Rs. 90,00,000

Cash balance lower limit = Rs. 20,000

Therefore the upper limit is equal to the lower limit of Rs. 20,000 plus the spread of a Rs. 23,000 i.e., Rs. 43,000.

The return point is equal to the lower limit of Rs. 20,000 plus the spread of Rs. 23,000/3 i.e., Rs. 20,000 + Rs. 23,000/3 = Rs. 27,667.

Therefore, the firm’s cash management policy should be based on lower and upper control limits of Rs. 20,000 and Rs. 43,000 respectively and the need to initiate action to keep will arise if it move outside this band.